Energia Kinetyczna Bryły Sztywnej

1. Bryła Sztywna: Definicja i Właściwości

1.1. Definicja Bryły Sztywnej

Bryła sztywna to pojęcie w mechanice klasycznej, odnoszące się do idealnego ciała, które nie zmienia swojego kształtu ani rozmiaru pod wpływem sił. Oznacza to, że odległości między dowolnymi punktami na tym ciele pozostają niezmienne, niezależnie od tego, jakie siły na nie działają. W praktyce bryła sztywna zachowuje swój kształt i wielkość podczas ruchu.

Chociaż w rzeczywistości każde ciało może się nieco odkształcić pod wpływem sił, to często te odkształcenia są na tyle małe, że można je pominąć. Uznanie ciała za sztywne ułatwia analizowanie jego ruchu i równowagi, upraszczając równania mechaniczne.

W bryle sztywnej odległości między dowolnymi dwoma punktami są zawsze takie same. To oznacza, że jeśli punkty A i B są od siebie oddalone o odległość d na początku ruchu, to w trakcie ruchu odległość ta pozostanie d.

Bez względu na to, jakie siły działają na bryłę sztywną, jej kształt i rozmiar pozostają niezmienione. W praktyce oznacza to, że geometria bryły nie zmienia się pod wpływem sił zewnętrznych.

Bryła sztywna może poruszać się w przestrzeni, przemieszczając się wzdłuż linii prostej (co nazywamy ruchem postępowym) oraz obracając się wokół osi (co nazywamy ruchem obrotowym). Połączenie tych dwóch rodzajów ruchu opisuje pełny ruch bryły sztywnej w przestrzeni.

1.2. Właściwości Bryły Sztywnej

• – Ruch Postępowy: Cała bryła porusza się jako jednostka, zachowując równoległość do swojej początkowej trajektorii. Ruch ten może być opisany jako ruch środka masy bryły, który porusza się w przestrzeni.
  
  Przykład: Wyobraź sobie, że masz prostokątną skrzynkę na kółkach, która porusza się wzdłuż prostej drogi. W tym przypadku, gdy skrzynka przemieszcza się do przodu, cały jej kształt porusza się wzdłuż tej samej linii prostej, zachowując równoległość do swojego początkowego kierunku. Oznacza to, że każda część skrzynki przemieszcza się w tym samym kierunku i z tą samą prędkością co inne części, a kąt i kształt skrzynki pozostają niezmienione.
  
  Na przykład boki i krawędzie skrzynki pozostają równoległe do siebie, a ich wzajemne odległości nie zmieniają się. W ruchu postępowym żadne części skrzynki nie zmieniają swojego wzajemnego układu, czyli nie ulegają deformacji ani przesunięciu w innym kierunku niż ten, w którym porusza się środek masy skrzynki.

• Ruch Obrotowy: Bryła może również obracać się wokół osi. W ruchu obrotowym każda cząstka bryły porusza się po okręgach lub elipsach o stałym promieniu wokół osi obrotu.
  
  Przykład: Wyobraź sobie wirujący drewniany bączek. Kiedy bączek kręci się, każda jego część porusza się po okręgu wokół osi, która przechodzi przez jego środek. Na przykład, jeśli bączek jest obracany wokół pionowej osi, wszystkie punkty na jego powierzchni opisują okręgi o stałym promieniu wokół tej osi. Oś obrotu jest nieruchoma, a bączek obraca się wokół niej, zachowując stały kształt i wielkość.
  

2. Energia Kinetyczna Bryły Sztywnej

Energia kinetyczna bryły sztywnej jest sumą dwóch składników: energii kinetycznej związanej z ruchem postępowym środka masy oraz energii kinetycznej związanej z ruchem obrotowym wokół środka masy. Ogólna formuła na energię kinetyczną bryły sztywnej jest następująca:

gdzie:

m to masa bryły,
v to prędkość środka masy,
I to moment bezwładności bryły względem osi obrotu,
ω to prędkość kątowa.

3. Ruch Postępowy i Energia Kinetyczna

3.1. Ruch Postępowy

W ruchu postępowym bryła porusza się wzdłuż ścieżki, a wszystkie jej punkty poruszają się z tą samą prędkością. Energia kinetyczna związana z ruchem postępowym jest opisana wzorem:

Ten składnik energii kinetycznej odpowiada za ruch całej bryły w przestrzeni.

4. Ruch Obrotowy i Energia Kinetyczna

4.1. Ruch Obrotowy

Ruch obrotowy polega na obrocie bryły wokół osi. Każdy punkt bryły porusza się po okręgu, którego promień jest odległością od osi obrotu. Energia kinetyczna związana z ruchem obrotowym jest opisana wzorem:

4.2. Moment Bezwładności

Moment bezwładności to miara oporu, jaki ciało stawia przy zmianie prędkości kątowej. Jest to zależne od rozkładu masy względem osi obrotu. W dużym uproszczeniu, można go porównać do masy w ruchu liniowym – podobnie jak większa masa oznacza większy opór przy zmianie prędkości, tak większy moment bezwładności oznacza większy opór przy zmianie prędkości kątowej.

Moment bezwładności zależy od dwóch głównych czynników: masy ciała oraz rozkładu masy względem osi obrotu. Im większa masa ciała, tym większy moment bezwładności. Masa umieszczona dalej od osi obrotu bardziej zwiększa moment bezwładności niż masa umieszczona bliżej osi.

Dla różnych kształtów brył, moment bezwładności przyjmuje różne wartości, co wynika z różnorodności w rozkładzie masy. Przykładowo, dla pręta obrotowego wokół środka moment bezwładności będzie mniejszy niż dla pręta obrotowego wokół końca, ponieważ masa jest równomiernie rozłożona wokół środka. Z kolei cienka obręcz obrotowa wokół osi symetrii będzie miała większy moment bezwładności niż dysk o tej samej masie i promieniu, ponieważ cała masa obręczy jest skoncentrowana na zewnętrznej krawędzi, dalej od osi obrotu. Pełna kula obrotowa wokół średnicy ma mniejszy moment bezwładności niż wydrążona kula o tej samej masie i promieniu, ponieważ masa pełnej kuli jest bardziej równomiernie rozłożona w stosunku do osi obrotu.

Dla różnych kształtów brył, moment bezwładności przyjmuje różne wartości. Oto kilka przykładów:

4.2.1 Twierdzenie Steinera

Twierdzenie Steinera, znane również jako twierdzenie o osiach równoległych, jest ważnym pojęciem w mechanice brył sztywnych. Twierdzenie to pozwala na obliczenie momentu bezwładności ciała wokół dowolnej osi równoległej do osi przechodzącej przez środek masy ciała. Jest ono szczególnie użyteczne w analizie ruchu obrotowego ciał, ponieważ umożliwia uproszczenie obliczeń w sytuacjach, gdzie obliczanie momentu bezwładności bezpośrednio wokół danej osi byłoby trudne.

Twierdzenie Steinera mówi, że moment bezwładności  ciała względem dowolnej osi równoległej do osi przechodzącej przez środek masy ciała jest równy sumie momentu bezwładności względem osi przechodzącej przez środek masy l_o i iloczynu masy ciała oraz kwadratu odległości między tymi osiami. Matematycznie, twierdzenie Steinera można zapisać jako:

gdzie:
I to moment bezwładności względem osi równoległej,
I_o to moment bezwładności względem osi przechodzącej przez środek masy,
m to masa ciała,
r to odległość między osiami.

Kula z przesuniętym środkiem obrotu

Załóżmy, że mamy kulę o promieniu r i masie m, obracającą się względem osi obrotu przesuniętej o odległość d od osi obrotu, która przechodziłaby przez środek masy tej bryły. 

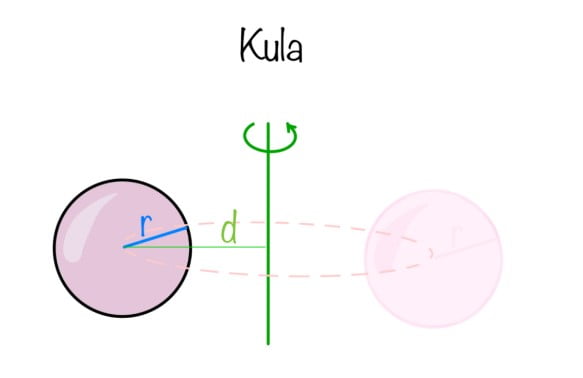
Moment bezwładności kuli względem jej własnej osi (przechodzącej przez środek masy) wynosi:

Stosując twierdzenie Steinera, moment bezwładności względem przesuniętej osi wynosi:

5. Energia Kinetyczna Bryły Sztywnej w Praktyce

5.1. Zastosowania w Mechanice

W mechanice klasycznej, połączenie ruchu postępowego i obrotowego jest istotne do analizy dynamiki ciał sztywnych. Równania ruchu i analizy energii kinetycznej są niezbędne w projektowaniu pojazdów, maszyn, czy w analizie ruchu planetarnego.

5.2. Zastosowania w Fizykach i Astronomii

– Ruch Planetarny: Analiza rotacji planet i gwiazd jest kluczowa w astronomii. Moment bezwładności i energia kinetyczna dla ruchu obrotowego są używane do badania dynamiki układów planetarnych.

6. Analiza Energetyczna Bryły Sztywnej

6.1. Energia Całkowita

Całkowita energia kinetyczna bryły sztywnej jest sumą energii dla ruchu postępowego i ruchu obrotowego. Przy obliczaniu całkowitej energii, uwzględnia się oba składniki:

6.2. Zmiany Energetyczne

W przypadku zmian w ruchu bryły, takich jak zmiana prędkości kątowej lub liniowej, całkowita energia kinetyczna może się zmieniać. Analiza takich zmian jest istotna w kontekście ruchu ciał w układach mechanicznych.

 7. Wnioski

Energia kinetyczna bryły sztywnej to istotny temat w mechanice klasycznej, który obejmuje zarówno ruch postępowy, jak i obrotowy. Rozumienie tej energii jest kluczowe w różnych dziedzinach, od inżynierii mechanicznej po astronomię. Obliczenia związane z energią kinetyczną pomagają w projektowaniu maszyn, analizie ruchów ciał niebieskich i badaniach dynamiki ciał sztywnych. Współczesne zastosowania tej wiedzy są szerokie i zróżnicowane, co podkreśla znaczenie tego tematu w nauce i technologii.

!! Co Powinieneś Umieć

• Definicja Bryły Sztywnej: Zrozumieć, że bryła sztywna to ciało, które nie ulega deformacji, a odległości między punktami pozostają stałe.
• Właściwości Bryły Sztywnej: Rozróżniać ruch postępowy (wszystkie punkty poruszają się z tą samą prędkością) i obrotowy (punkty poruszają się po okręgach wokół osi).
• Energia Kinetyczna: Znać wzór: E_k = 1/2mv² + 1/2Iω² i rozumieć, że składa się ona z energii kinetycznej ruchu postępowego i obrotowego.
• Ruch Postępowy: Umieć opisać ruch postępowy bryły i znać wzór na jego energię kinetyczną E_kp=1/2mv².